長期の時系列分析例通常版

このページでは、JINS MEME通常版の60秒間隔データから短期（日・週）の区間代表値を抽出し、長期間（月・年）の時系列分析をする方法を説明します。

長期時系列分析を実施するにあたっての注意点

指標をある程度のまとまった期間（1日、1週間）でサマライズし、ユーザー間の相対差に着目したり、ユーザー内の長期推移に着目することでユーザーの状態やその推移を見たいというニーズがあったとします。この場合に注意が必要な点として、よほどコントロールされた実験でない限りユーザーや日によって装着時間が異なったり、データの欠落が必ず発生しています。例えば1日のまばたきの回数を算出するのに単純に回数を合計しただけの場合、前記の装着時間・欠落時間の影響を直接受けてしまうため、精度が大きく下がります。そのため代表値の算出は単純にパーテションの算術合計や算術平均を取るのではなく、分布を経由して算出する必要があります。

処理の概要

(1) ヒストグラムの確認

理論的に無理なく、かつ技術的にフィッティングしやすい分布がどれか（例: 正規分布、ガンマ分布、指数分布）を確認します。指標によっては累積度数分布を取ることでより安定したプロットを得ることが可能です。

(2) 代表値の抽出

分布の形状毎に代表値を抽出する方法が異なります。また、データの状態によっては手法を変更したほうがより安定した代表値を抽出することが可能になることもあります。

• 正規分布: きれいな分布になっている時は一番素直に平均を取得するのが良いですが、外れ値が強い時は中央値に切り替えます。
  • 第1選択: 平均
  • 第2選択: 中央値
• ガンマ分布: ガンマ分布を決定する係数は、数学的には形状母数 k、尺度母数 θ ですが、ここでは代表値を得るのが目的なので以下のような手段を取ります。
  • 第1選択: 分布のノンパラメトリック推定→ピーク位置の算出
  • 第2選択: 中央値、もしくは低めのQuantile(30-40%)
• 指数分布: 0付近で最大となり漸減する指標に対しては以下の順番で試します。
  • 第1選択: 対数プロットの傾き
  • 第2選択: Quantile(90%/95%/99%)

処理例その1...頭部運動回数（左右）の週依存

頭部運動回数（左右）（＝首フリ）は周りに注意を向けたり、会話したり、いろいろなものを閲覧したりと、フィジカルな活性度を測るのに適した指標です。歩数は歩いている時にしかカウントされませんが、頭部運動は歩行に加えて座っている状態における小さなアクティビティも拾うことができます。この頭部運動の代表値を取得し、ユーザーごとの推移を取得することを目標としたPythonによる分析のサンプル処理を以下に示します。

処理するデータ

60秒間隔データにユーザーごとの個別IDを付与したデータフレーム(data_df)を想定します。

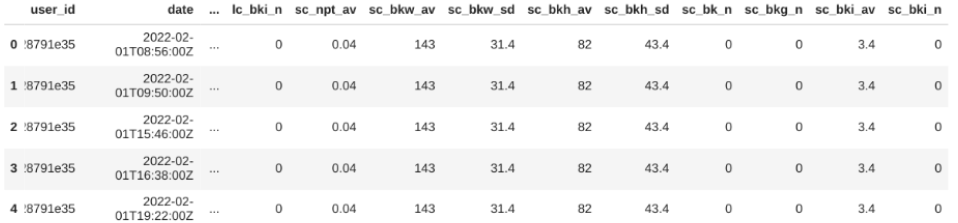
下処理

週単位でデータを比較するので、週番号をアサインします。

import pandas as pd
import numpy as np

data_df['datetime'] = pd.to_datetime(data_df.date)
data_df['week'] = data_df['datetime'].dt.isocalendar().week
data_df["user_id_short"] = data_df["user_id"].str[:5] #表示用に簡素化

以下のような正しく装着している状態（装着時間がある程度あり、メガネが変な角度を向いていない）のみを残すフィルタをかけます。

data_filtered_df = data_df.query("wea_s >= 20 & tl_yav >= -45 & tl_yav <= 90 & tl_xav >= -45 & tl_xav <= 45")

ヒストグラム化(1)

指数分布なので、対数プロットで週毎の分布を比較します。

import seaborn as sns

#log
sns.set_style("darkgrid")
sns.set_context("talk")
g = sns.displot(
    data_filtered_df, x = "hm_yo", hue = "week", palette = "dark", col="user_id_short", kind='kde', col_wrap=6
)
g.set(xlim=(0, 150))
g.set(ylim=(1e-6, 1e-3))
for axes in g.axes:
    axes.set_yscale('log')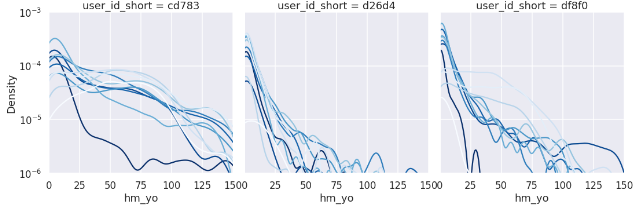

おおよそ差は出ていますが、これでは比較が難しいので累積度数に変換してみます。

ヒストグラム化(2)

累積度数は(1)パーテション毎に順位をつけ、(2)パーテションの件数を求め、(3)1を2でそれぞれ割る、ことで求めることができます。

#パーテション毎に降順で順位をつける
idx = "hm_yo"
part = "week"
tmp_df = data_filtered_df

ranked_df = tmp_df.assign(
        group_rank=tmp_df.sort_values([idx], ascending=False)
        .groupby(["user_id", part])
        .cumcount() + 1
)

#パーテション毎の件数を数える
group_df = tmp_df[["user_id", part,"date"]].groupby(["user_id", part]).count().reset_index().rename(columns={'date': 'count'})

#INNER JOINして件数で割ることで累積確率に変換する
merged_df = pd.merge(ranked_df, group_df, on=["user_id", part])
merged_df["cdf"] = merged_df["group_rank"] / merged_df["count"]

#plot
sns.set_style("darkgrid")
sns.set_context("talk")

g = sns.relplot(
    data=merged_df,
    x=idx, y="cdf",
    hue=part, col="user_id_short", palette = "Blues", #dark
    kind="line" ,col_wrap=6
)
g.set(xlim=(0, 150))
g.set(ylim=(1e-3, 1))
for axes in g.axes:
    axes.set_yscale('log')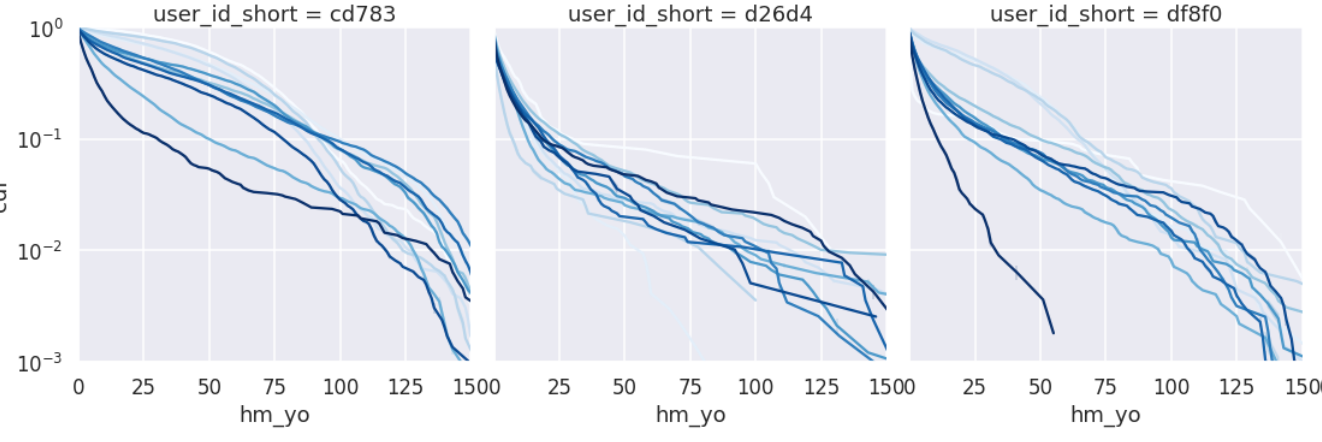

こちらのほうがより安定して週比較をできそうです。ただし、代表値を傾きで取るには線形性が弱いので、Quantileで取ることにします。

※活動量の累積確率分布を取り、傾きを議論することについての詳細な分析が日立中央研究所の研究で報告がされています。

代表値の抽出とプロット

90% Quantile、99% Quantileで代表値を抽出し、推移をプロットします。

#パーテション毎にPercentileを取る
idx = "hm_yo"
part = "week"
tmp_df = data_filtered_df

# 90% Percentile
def q90(x):
    return x.quantile(0.9)

# 99% Percentile
def q99(x):
    return x.quantile(0.99)

#週別に代表値にAggする
quantile_df = tmp_df[["user_id_short", part, "hm_yo"]].groupby(["user_id_short", part], as_index=False).agg(
    hm_q90 = ('hm_yo', q90), hm_q99 = ('hm_yo', q99))

#plot
grid = sns.FacetGrid(quantile_df, col="user_id_short", col_wrap=6)
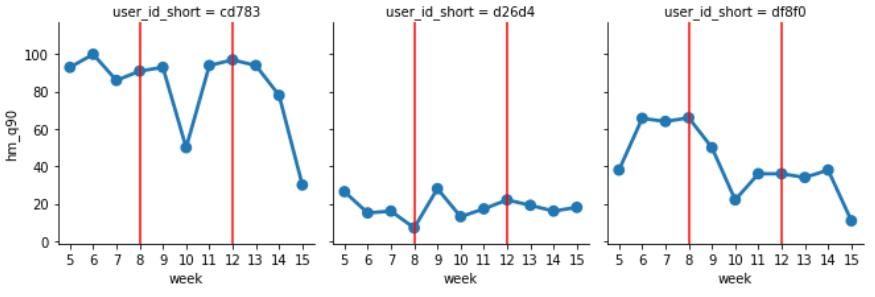
grid.map(sns.pointplot, 'week', 'hm_q90') #本当はorderはセットしておいたほうが良い , order = [0,1,2]
#縦線を入れてみる場合
for axes in grid.axes:
    axes.axvline(3, c='r')
    axes.axvline(7, c='r')

下記が週毎の90％Quantileの推移を示しており、ランダムに暴れたりせずに人による差や推移が安定して取れていることが分かります。

処理例その2...視線移動回数（左右）の週依存

視線移動回数（左右）は注意や思考と強く相関があり、メンタルの活性度を測るのに適した指標です。この代表値を取得し、ユーザーごとの推移を取得することを目標としたPythonによる分析のサンプル処理を以下に示します。

処理するデータ

60秒間隔データにユーザーごとの個別IDを付与したデータフレーム(data_df)を想定します。

下処理

週単位でデータを比較するので、週番号をアサインします。また、視線移動は移動量に応じて視線移動小回数(左右)と視線移動大回数(左右)にカウントが分かれているので足しておきます。

import pandas as pd
import numpy as np

data_df['datetime'] = pd.to_datetime(data_df.date)
data_df['week'] = data_df['datetime'].dt.isocalendar().week 
data_df["user_id_short"] = data_df["user_id"].str[:5] #表示用に簡素化

data_df["em_rl"] = data_df["ems_rl"] + data_df["eml_rl"]

以下のような正しく装着している状態（装着時間がある程度あり、メガネが変な角度を向いていない）のみを残すフィルタをかけます。眼電位系の場合は、nis_s <= 10 のフィルタを追加するとよりノイズの少ないデータのみで比較ができます。

data_filtered_df = data_df.query("wea_s >= 20 & tl_yav >= -45 & tl_yav <= 90 & tl_xav >= -45 & tl_xav <= 45" & "nis_s <= 10")

ヒストグラム化

週毎にプロットし比較してみます。

import seaborn as sns
tmp_df = data_filtered_df

#kdeのみプロット
sns.set_style("darkgrid")
sns.set_context("talk")
g = sns.displot(
    tmp_df, x = "em_rl", hue = "week", palette = "Blues", col="user_id_short", kind='kde', col_wrap=6,
)
g.set(xlim=(0, 120))
g.set(ylim=(0, 0.0003))
#縦線を入れてみる場合
for axes in g.axes:
    axes.axvline(15, c='r')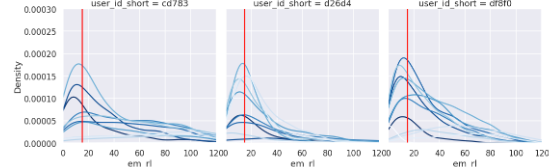

ガンマ分布のような形状を示していることがわかります。

代表値の抽出とプロット

ノンパラメトリックな手法（kde: カーネル推定）により分布関数を算出し、ピーク位置を抽出し、週依存に変換します。

import scipy.stats as stats

#パーテション毎にPercentileを取る
idx = "em_rl" 
part = "week"
tmp_df = data_filtered_df

#kdeを行い、最大値を取る地点を返す関数
def kde_max(x):
    #npでフィッティング
    nparam_density = stats.gaussian_kde(x)
    #x作る
    aryx = np.linspace(0, 200, 201)
    #y作る
    aryy = nparam_density(aryx)   
    
    #y最大の引数をx配列に渡してxの取得
    return aryx[aryy.argmax()]

#週別に代表値にAggする
quantile_df = tmp_df[["user_id_short", part, "em_rl"]].groupby(["user_id_short", part], as_index=False).agg(
    em_kmax = ('em_rl', kde_max))

#plot
grid = sns.FacetGrid(quantile_df, col="user_id_short", col_wrap=6)
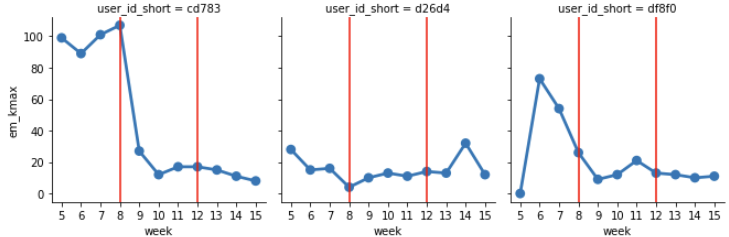
grid.map(sns.pointplot, 'week', 'em_kmax') #orderはセットしておいたほうが良い , order = [0,1,2]
#縦線を入れてみる場合
for axes in grid.axes:
    axes.axvline(3, c='r')
    axes.axvline(7, c='r')

下記が週毎のピーク位置の推移を示しており、ランダムに暴れたりせずに人による差や週推移を議論できる状態にできました。